双曲函数有哪些性质?

双曲函数是一类比较特殊的函数, 这类函数与我们熟悉的三角函数有类似的性质, 但又不完全相同. 了解双曲函数的基本性质, 有助于我们更快解决某些问题.

双曲函数的定义

双曲正弦 $\sinh x=\frac{ e ^x- e ^{-x}}{2}$,
双曲余弦 $\cosh x=\frac{ e ^x+ e ^{-x}}{2}$,
双曲正切 $\tanh x=\frac{\sinh x}{\cosh x}=\frac{ e ^x- e ^{- x }}{ e ^x+ e ^{- x }}$

双曲余切 $\operatorname{coth} x=\frac{\cosh x}{\sinh x}=\frac{e^x+e^{-x}}{e^x-e^{-x}}=\frac{e^{2 x}+1}{e^{2 x}-1}$
双曲正割 $\operatorname{sech} x=\frac{1}{\cosh x}=\frac{2}{e^x+e^{-x}}=\frac{2 e^x}{e^{2 x}+1}$
双曲余割 $\operatorname{csch} x=\frac{1}{\sinh x}=\frac{2}{e^x-e^{-x}}=\frac{2 e^x}{e^{2 x}-1}$

双曲函数的图像

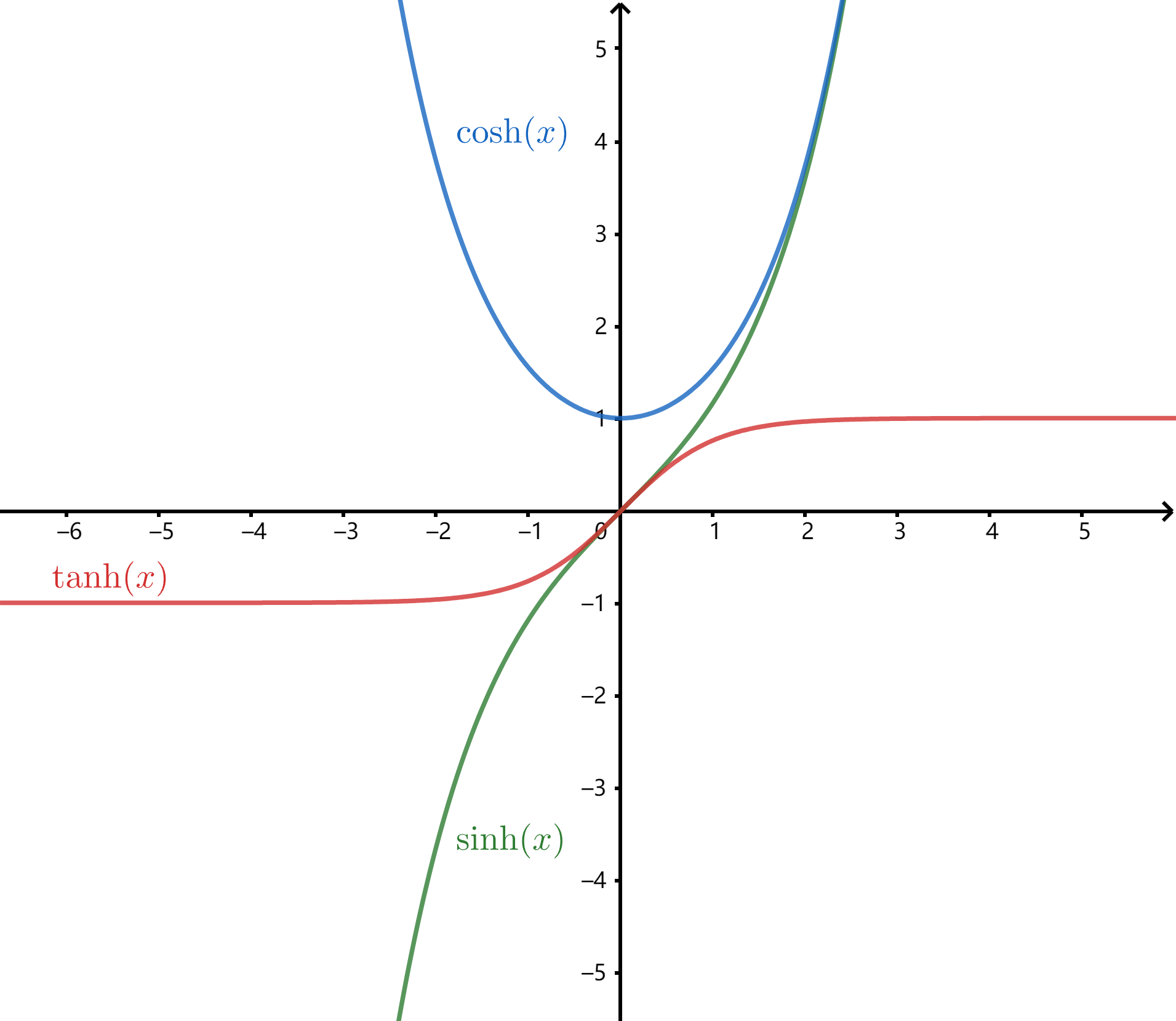
从图像, 我们可以看到双曲正弦和双曲正切是奇函数, 单调递增. 双曲余弦是偶函数, 在y轴左边单调递减, 在y轴右边单调递增. x=0时取得最小值1.

双曲函数的诱导公式

$\cosh ^2 x-\sinh ^2 x=1$

双曲函数的和差角公式

$$ \begin{aligned} & \sinh (x+y)=\sinh x \cosh y+\cosh x \sinh y \\ & \cosh (x+y)=\cosh x \cosh y+\sinh x \sinh y \\ & \tanh (x+y)=\frac{\tanh x+\tanh y}{1+\tanh x \tanh y} \end{aligned} $$

双曲函数的倍角公式

$$ \begin{aligned} & \sinh 2 x=2 \sinh x \cosh x \\ & \cosh 2 x=\cosh ^2 x+\sinh ^2 x=2 \cosh ^2 x-1=2 \sinh ^2 x+1 \end{aligned} $$

双曲函数的导数公式

$$ \begin{aligned} \frac{ d }{ d x} \sinh x & =\cosh x \\ \frac{ d }{ d x} \cosh x & =\sinh x \\ \frac{ d }{ d x} \tanh x & =1-\tanh ^2 x=\operatorname{sech}^2 x=\frac{1}{\cosh ^2 x} \end{aligned} $$

双曲函数的积分公式

$$ \begin{aligned} & \int \sinh x d x= \cosh x+C \\ & \int \cosh x d x=\sinh c x+C \\ & \int \tanh x d x= \ln (\cosh x)+C \\ & \int \operatorname{coth} x d x= \ln |\sinh x|+C \\ & \int \operatorname{sech} x d x= \arctan (\sinh x)+C \\ & \int \operatorname{csch} x d x= \ln \left|\tanh \frac{ x}{2}\right|+C \end{aligned} $$

双曲函数的级数展开(泰勒公式)

$$ \begin{aligned} & \sinh x=x+\frac{x^3}{3 !}+\frac{x^5}{5 !}+\frac{x^7}{7 !}+\cdots=\sum_{n=0}^{\infty} \frac{x^{2 n+1}}{(2 n+1) !} \\ & \cosh x=1+\frac{x^2}{2 !}+\frac{x^4}{4 !}+\frac{x^6}{6 !}+\cdots=\sum_{n=0}^{\infty} \frac{x^{2 n}}{(2 n) !} \\ & \tanh x=x-\frac{x^3}{3}+\frac{2 x^5}{15}-\frac{17 x^7}{315}+\cdots=\sum_{n=1}^{\infty} \frac{2^{2 n}\left(2^{2 n}-1\right) B_{2 n} x^{2 n-1}}{(2 n) !},|x|<\frac{\pi}{2} \end{aligned} $$