mathematica在高等数学中的应用

函数极限计算

计算函数$f(x)$在$x$趋于时$a$的极限的基本格式为Limit[f, x->a]
计算左极限的基本格式为Limit[f, x->a, Direction -> "FromBelow"]
计算右极限的基本格式为Limit[f, x->a, Direction -> "FromAbove"]

例

In[1]:= Limit[Sin[x]/x, x -> 0](*计算重要极限sinx/x*)

Out[1]= 1

In[1]:= Limit[RealAbs[x]/x, x -> 0, Direction -> "FromAbove"](*计算|x|/x的右极限*)

Out[1]= 1

In[2]:= Limit[RealAbs[x]/x, x -> 0, Direction -> "FromBelow"](*计算|x|/x的左极限*)

Out[2]= -1

函数的导数计算

计算对$x$的偏导数$\partial f/\partial x$ 的格式为 D[f, x]
计算对$x$的$n$阶偏导${{\partial }^{n}}f/\partial {{x}^{n}}$的基本格式为D[f,{x,n}]
计算混合偏导数$\frac{{{\partial }^{n+m}}f}{\partial {{x}^{n}}\partial {{y}^{m}}}$的基本格式为D[f,{x,n},{y,m}]
计算全微分的基本格式为 Dt[f]

例

$z=\ln \sqrt{x^2+y^2}$, 求$\frac{\partial z}{\partial x},\frac{\partial z}{\partial y},\frac{{{\partial }^{2}}z}{\partial x\partial y}$

In[1]:= Clear[x, y]; z = Log[Sqrt[x^2 + y^2]]; 
D[z, x] 
D[z, y] 
D[z, x, y]

Out[1]= x/(x^2 + y^2)

Out[2]= y/(x^2 + y^2)

Out[3]= -((2 x y)/(x^2 + y^2)^2)

$z=\sqrt{x}+\sqrt{y}$, 求$ dz$.

In[1]:= Clear[x, y]; z = Sqrt[x] + Sqrt[y]; Dt[z]

Out[1]= Dt[x]/(2 Sqrt[x]) + Dt[y]/(2 Sqrt[y])

计算不定积分和定积分

Integrate[f[x],x]表示求 $f$ 对 $x$ 的不定积分
Integrate[f[x],{x,a, b}]表示求 $f$ 在区间$[a,b]$ 的定积分

例

计算$\sin x e^x$的不定积分和在区间[0, 5]上的定积分.

In[1]:= Integrate[Sin[x]*E^x, x]

Out[1]= 1/2 E^x (-Cos[x] + Sin[x])

In[2]:= Integrate[Sin[x]*E^x, {x, 0, 5}]

Out[2]= 1/2 (1 + E^5 (-Cos[5] + Sin[5]))

计算重积分

求二重积分的基本格式为 Integrate[f,{x, xmin, xmax},{y, ymin, ymax}]

例

$\iint\limits_{D}{(1-x-y)dxdy},D:x\ge 0,y\ge 0,x+y\le 1$

In[1]:= Clear[x, y]; 
Integrate[1 - x - y, {x, 0, 1}, {y, 0, 1 - x}]

Out[1]= 1/6

$\iint_{D}{\left( 1-{{x}^{2}}-{{y}^{2}} \right)}dxdy\text{,}\quad D\text{:}{{x}^{2}}+{{y}^{2}}\le 1$

In[1]:= Clear[x, y]; 
Integrate[1 - x^2 - y^2, {x, y} \[Element] Disk[]]
(*其中Disk[]表示单位圆盘区域*)

Out[1]= \[Pi]/2

计算微分方程

求解关于$x,y$的微分方程的基本格式为 DSolve[eqn, y[x], x], 其中 $x$ 为独立变量.
求解给定初值y[0]=a的微分方程的格式为 DSolve[{eqn, y[0] == a}, y[x], x]

例

求微分方程
$$\left\{ \begin{align} & y''+y+\sin x=0 \\ & y(0)=1,\ y'(0)=1 \\ \end{align} \right.$$的解.

In[1]:= Clear[x, y]; 
DSolve[{y''[x]+y[x]+Sin[x] == 0, y[0] == 1, y'[0] == 1}, y[x] ,x]

Out[1]= {{y[x] -> 
1/4 (4 Cos[x] + 2 x Cos[x] + 2 Sin[x] + 2 Cos[x]^2 Sin[x] - 
   Cos[x] Sin[2 x])}}

求解微分方程$\left(1+e^x\right) \frac{d y}{d x}-y=0$

In[1]:= Clear[x, y]; DSolve[(1 + E^x)*y'[x] - y[x] == 0, y[x], x]

Out[1]= {{y[x] -> (E^x C[1])/(1 + E^x)}}

2D绘图

画出$f(x)$在$[a,b]$区间上的图形格式为Plot[f, {x,a,b}]
画出多个函数f1,f2,……在[a,b]区间上的图形Plot[{f1,f2, ... },{x,a,b}]
画出一个极坐标方程表示的函数图形 PolarPlot[r[t],{t,min,max}]
画出一个参数方程所表示的函数图形 ParametricPlot[{g[t],h[t]},{t,min,max}]

例

绘制正切函数图形
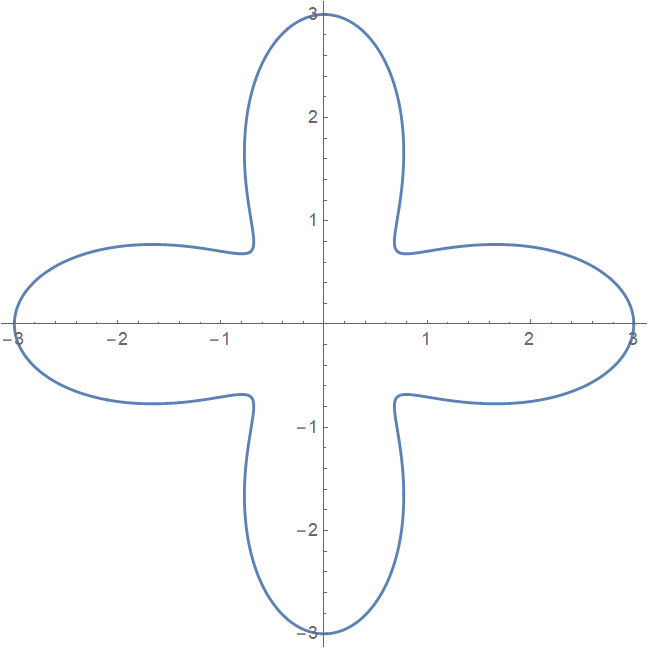
画出四叶草函数图形$r=2 + \cos 4x$
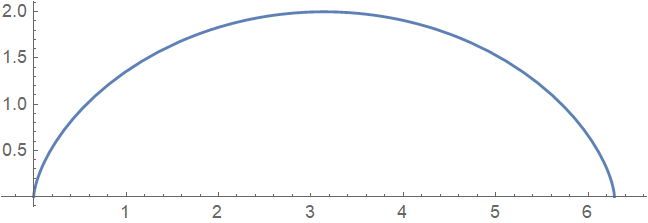
画出摆线的函数图形.
$$ \left\{\begin{array}{l} x=1-\sin t \\ y=1-\cos t \end{array}\right. $$

Plot[Tan[x], {x, -5, 5}]

PolarPlot[2 + Cos[4*x], {x, 0, 2*Pi}]

ParametricPlot[{t - Sin[t], 1 - Cos[t]}, {t, 0, 2 Pi}]

绘图结果为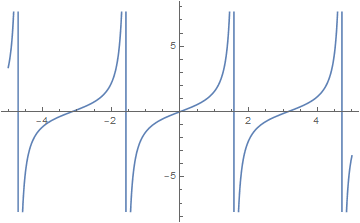

3D绘图

绘制3D曲面的基本格式为Plot3D[f(x,y),{x,a,b},{y,c,d}]

例

$f(x,y)={{x}^{2}}-{{y}^{2}}(-10\le x\le 10,-10\le y\le 10)$, 绘制$f(x,y)$的图形.

Plot3D[x^2-y^2,{x,-10,10},{y,-10,10}]

输出结果为