问题89: 如何计算渐近线方程?

首先需要知道渐进线如何定义:

曲线上一点M沿曲线无限远离原点或无限接近无穷间断点时，如果M到一条直线的距离无限趋近于零，那么这条直线称为这条曲线的渐近线

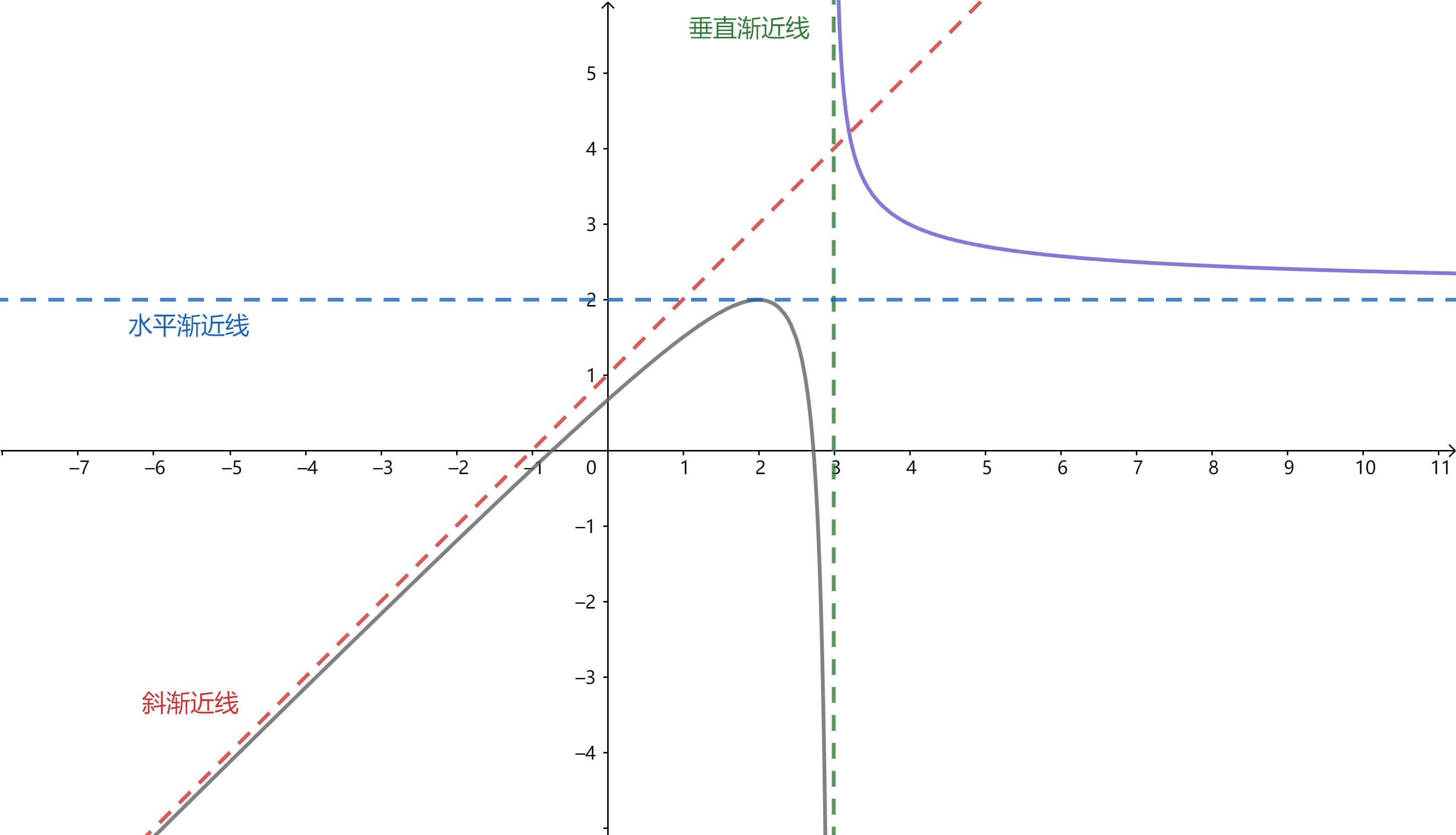
按照这个定义, 渐近线分成三类:

1. 水平渐近线.
2. 垂直渐近线.
3. 斜渐近线.

以下分别给出这三类渐近线的计算方法.

计算水平渐近线

计算水平渐近线只需要求出$x\rightarrow ∞$时的极限就可以了. 对一个函数而言, 最多有两条水平渐近线.

计算垂直渐近线

计算垂直渐近线的关键是找到无穷间断点. 一般是分母为0或者对数部分为0的那些点.

计算斜渐近线

要计算斜渐近线, 先计算出函数与x比的极限$\lim _{x \rightarrow \infty} \frac{f(x)}{x}$, 就是渐近线的斜率$k$, 然后计算函数与$kx$差的极限$b =\lim _{x \rightarrow \infty} f(x)-k x$, 就是斜渐近线的y截距, 这样渐近线就是$y=kx+b$.

注意: 一个函数的斜渐近线和水平渐近线最多有两条, 垂直渐近线可能有无数条.

例:

添加微信可以更快获取解答（请注明有偿答疑）