问题88: 如何区分驻点/极值点/最值点/拐点?

驻点

驻点分是切线与x轴平行的点, 也就是导数为0的点. 例$y=(x-1)^2$有一个驻点$x=1$.

另外, 某些教材(主要是某些国外版本教材)也把切线与y轴平行的点认为是驻点. 例如$x=0$是$y=\sqrt{x}$的一个驻点.

极值点

极值点是一个局部最值, 也就是在这一点, 函数在某个邻域内取得最值. 不要求可导, 但是必须在某个邻域内有定义.

例如, $y=x^2$在$x=0$处取得极小值. 但是, $y=\sqrt{x}$在$x=0$处不是极小值, 因为函数在左邻域内没有定义.

最值点

函数在这一点有定义, 且是函数的最大值或者最小值, 不要求函数在这一点可导.

例如, $y=|x|$在$x=0$取得最小值.

拐点

函数凹凸性改变的点, 不要求函数可导.

测一测

1. 驻点处函数一定可导. ( )
2. 最值点导数为0. ( )
3. y=|x|有一个极值点. ( )
4. y=x^3有个拐点. ( )
5. 驻点一定是极值点. ( )
6. 最值点一定是极值点. ( )

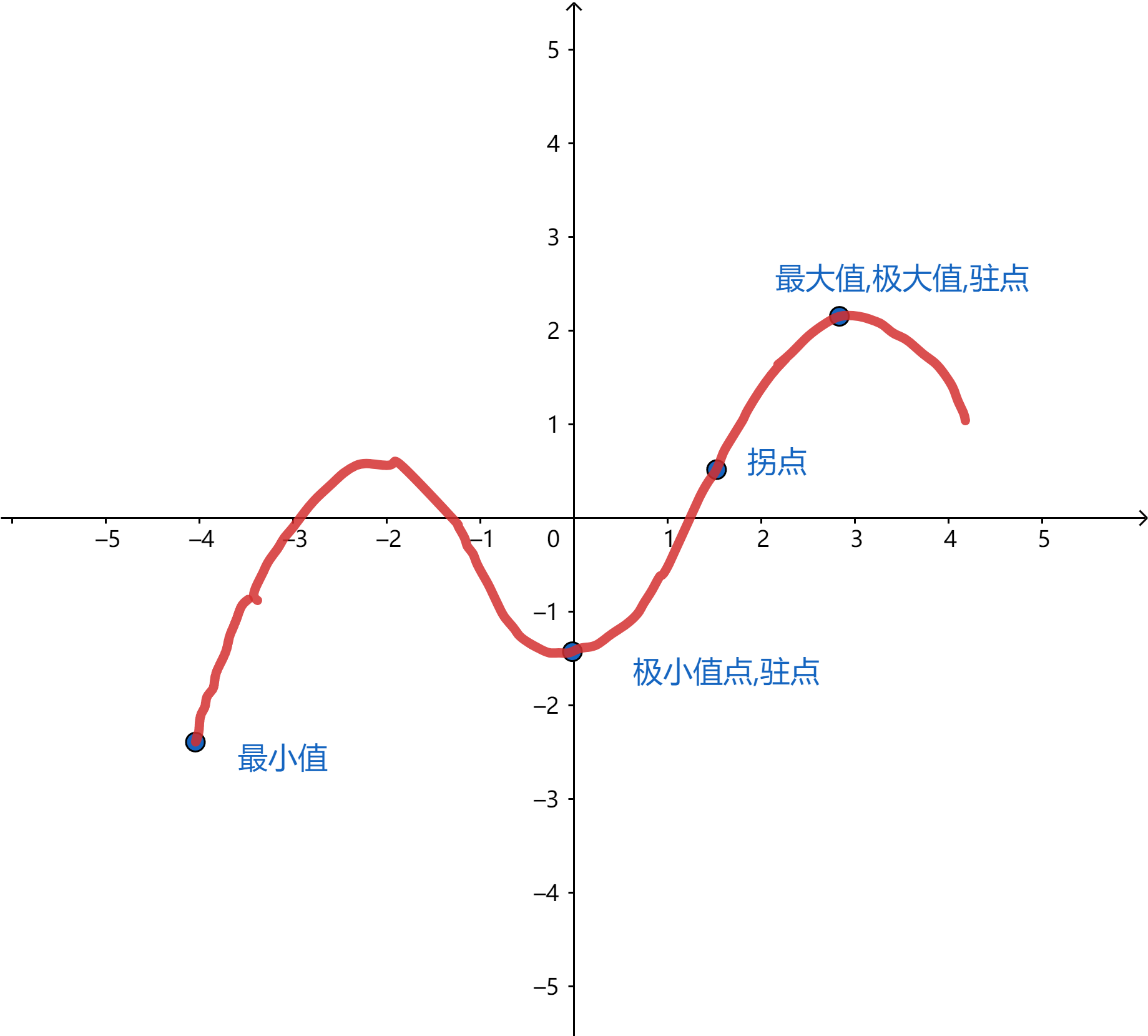
答案: 1. √ 2.× 3. √ 4. √ 5. × 6. ×

添加微信可以更快获取解答（请注明有偿答疑）