问题581: 求和

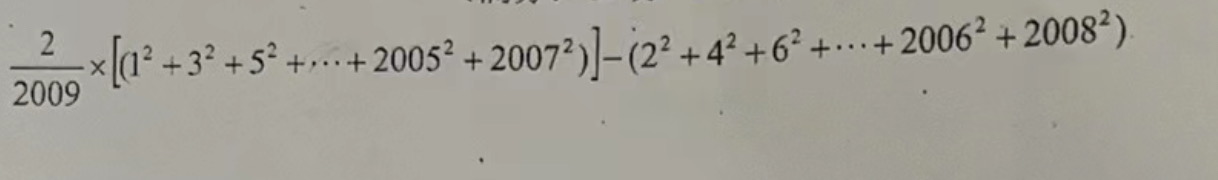
$$ \begin{aligned} & \frac{2}{2009} \times\left[\left(1^2+3^2+5^2+\cdots+2005^2+2007^2\right)\right]-\left(2^2+4^2+6^2+\cdots+2006^2+2008^2\right) \\ = & \frac{2}{2009} \times\left[\sum_{n=1}^{2008} n^2-\sum_{n=1}^{1004}(2 n)^2\right]-\sum_{n=1}^{1004}(2 n)^2 \\ = & \frac{2}{2009} \times \sum_{n=1}^{2008} n^2-\frac{2011 \times 4}{2009} \sum_{n=1}^{1004} n^2 \\ = & \frac{2}{2009} \times \frac{2008 \times 2009 \times 4017}{6}-\frac{2011 \times 4}{2009} \times \frac{1004 \times 1005 \times 2009}{6} \\ = & 2008 \times 1339-4 \times 2011 \times 502 \times 335 \\ = & -1350070768 \end{aligned} $$

添加微信可以更快获取解答（请注明有偿答疑）