问题559: 求极限

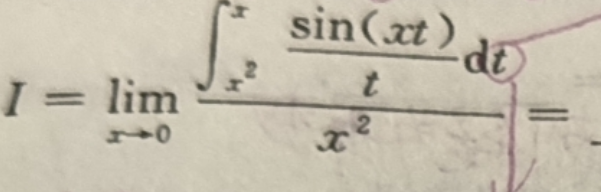
$$ \begin{aligned} & I=\lim _{x \rightarrow 0} \frac{\int_{x^2}^x \frac{\sin (t)}{t} d t}{x^2} \\ & =\lim _{x \rightarrow 0} \frac{\int_{x^3}^{x^2 } \frac{\sin u}{u/x} d(u/x)}{x^2} \quad(令 u=x t) \\ & =\lim _{x \rightarrow 0} \frac{\int_{x^3}^{x^2} \frac{\sin u}{u} d u}{x^2} \\ & =\lim _{x \rightarrow 0} \frac{\left(x^2-x^3\right) \frac{\sin \xi}{\xi}}{x^2} \quad \text { (积分中值定理) } \\ & =\lim _{x \rightarrow 0} \frac{x^2-x^3}{x^2} \\ & =1 \\ & \end{aligned} $$

添加微信可以更快获取解答（请注明有偿答疑）