计算二重积分∬_Dln(1+x^2+y^2)dx dy
计算二重积分 $\iint_D \ln \left(1+x^2+y^2\right) \mathrm{d} x \mathrm{~d} y$, 其中 $D$ 是单位圆域：
$$ x^2+y^2 \leq 1 \text {. } $$
问题
解答
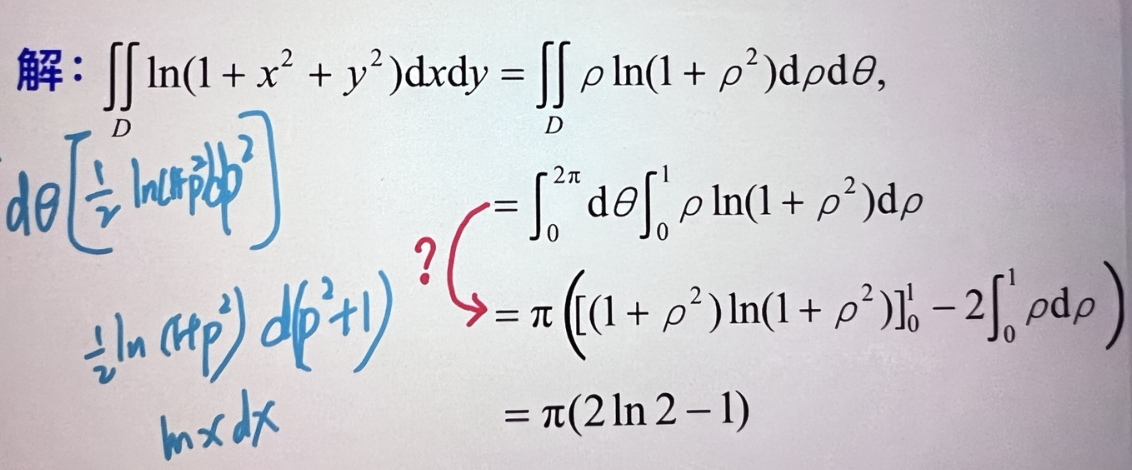
添加微信
可以更快获取解答（请注明有偿答疑）
最后修改于1月3日
提交新的问题
前一篇：设z=f(x/y,x^2+y^2),其中f具有一阶连续偏导数,则∂z/∂y=().
下一篇：求证:(1+1/n-1)^n>(1+1/n)^n+1