问题536: 求长方形的面积

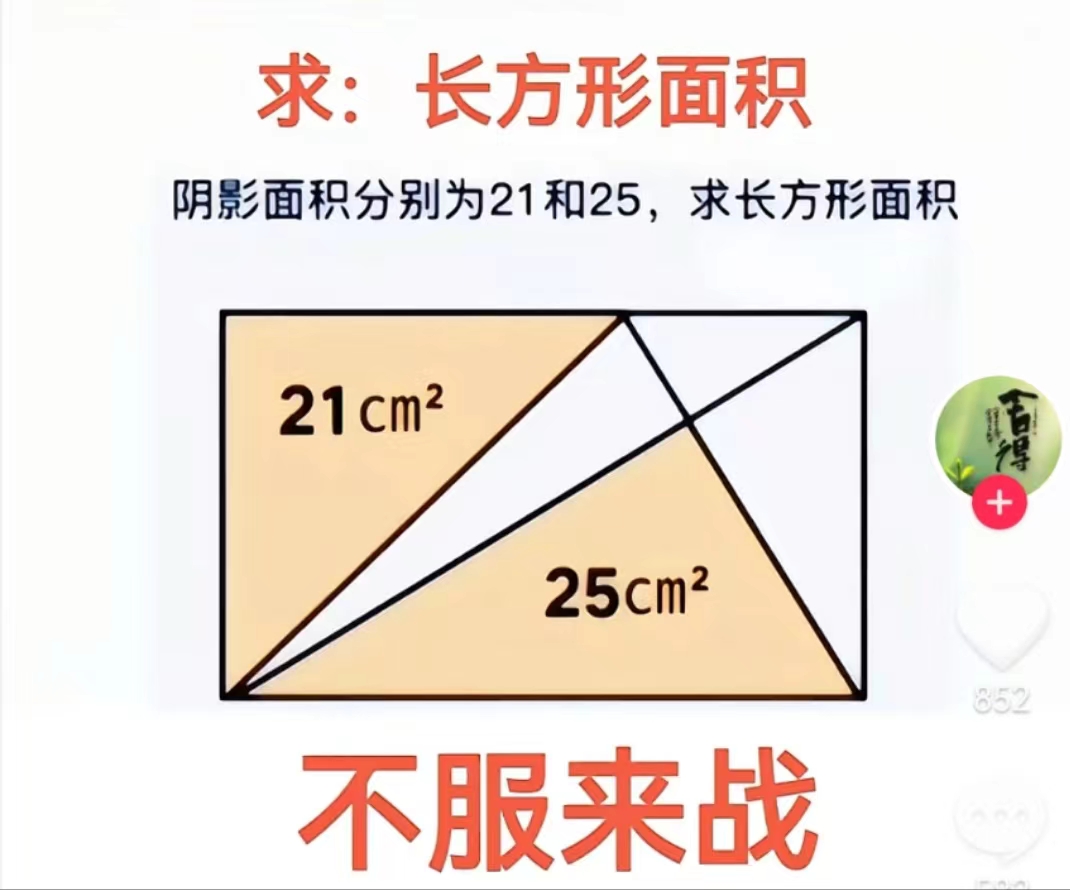
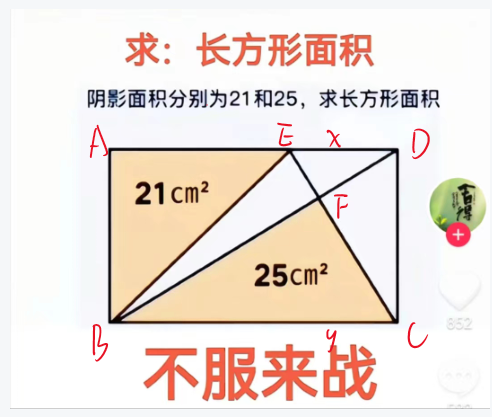
设$ED=x, BC=y$.

$$ \begin{aligned} & \text { 则 } S_{\triangle A B E}=\frac{1}{2} A B \cdot A E=\frac{1}{2} A B \cdot(y-x)=21 \\ & A B=\frac{42}{y-x} \\ & S_{\triangle B F C}=\frac{1}{2} B C \cdot h_{B C}=\frac{1}{2} B C \cdot A B \cdot \frac{y}{x+y}=\frac{1}{2} \cdot y \cdot \frac{42}{y-x} \cdot \frac{y}{y+x}=25 \\ & \text { 得 } 4 y^2=25 x^2 \cdot \text { 即 } \frac{x}{y}=\frac{2}{5} \\ & S_{ A B C D}=A B \cdot B C=\frac{42}{y-x} \cdot y=\frac{42}{1-\frac{1}{y}}=\frac{42}{1-\frac{2}{5}}=70 \mathrm{~cm}^2 . \end{aligned} $$

添加微信可以更快获取解答（请注明有偿答疑）