问题477: 如图1，在平面直角坐标系中，已知点A坐标为(-3,0)，点B坐标为 (5,0),点C在一象限，CA=CB,∠ACB=90°.

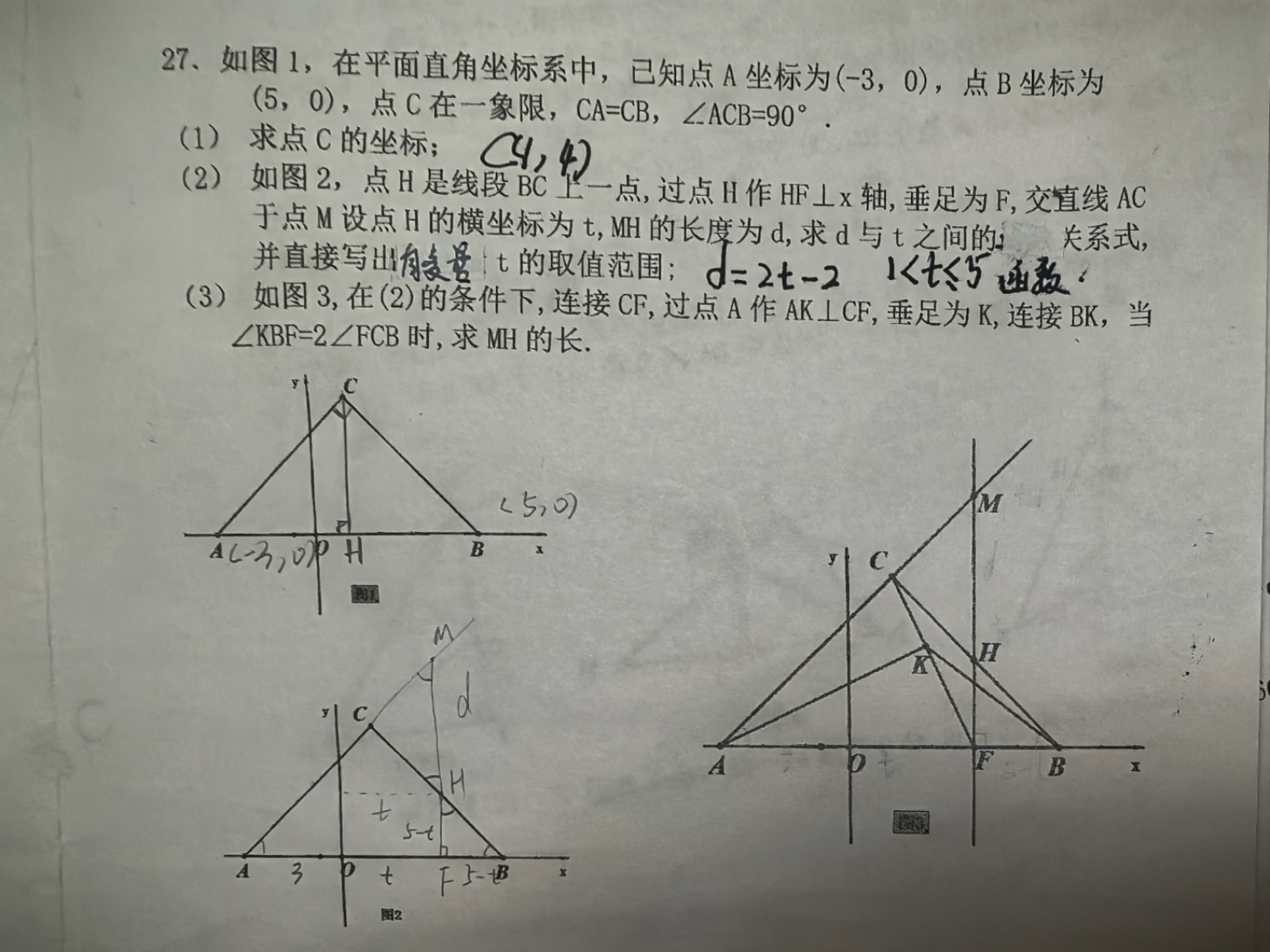
如图1，在平面直角坐标系中，已知点A坐标为(-3,0)，点B坐标为
(5,0),点C在一象限，CA=CB,∠ACB=90°.
(1)求点C的坐标；
(2)如图2，点H是线段BC上一点，过点H作HF⊥x轴，垂足为F,交直线AC
于点M设点H的横坐标为t,MH的长度为d,求d与t之间的函数关系；
并直接写出t的取值范围；

(3)如图3，在(2)的条件下，连接CF,过点A作AK⊥CF,垂足为K,连接BK,当
∠KBF=2∠FCB 时，求 MH 的长.