问题435: 离散型随机变量题：一款双人在线对战游戏，

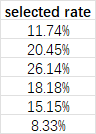
离散型随机变量题：一款双人在线对战游戏，六个角色可供玩家选择。两个玩家从这六个角色中各选择一个进行游戏比赛。由于每个游戏角色的受欢迎程度不一样，所以六个游戏角色被选中的概率也都不一样。六个游戏角色被玩家选中的概率分别为：
A: 11.74%
B: 20.45%
C: 26.14%
D: 18.18%
E: 15.15%
F: 8.33%
接下来该游戏有一场竞赛，共比赛30场，玩家从这六个角色中选择60次。请问排名最后的两个角色A和F中任何一个未被选中的概率是多少？