3. The course notes discuss right- and left-hand Reimann sum
The course notes discuss right- and left-hand Reimann sums. Consider now the midpoint Riemann sum defined by $M_n=\sum_{i=1}^n f\left(\bar{x}_i\right) \Delta x$, where $\bar{x}_i=\frac{1}{2}\left(x_{i-1}+x_i\right)$. Consider
$$ I=\int_0^2\left(2 x+x^2\right) d x $$
(a) Find $M_n$ and use the midpoint Riemann sum to show that $I=\frac{20}{3}$.
(b) What is the minimum number of intervals that are required so that $M_n$ is within $\varepsilon$ units from $I$ (where $\varepsilon \in \mathbb{R}, \varepsilon>0$ )? Use your results to determine the number of intervals required so that $\left|M_n-I\right|<0.001$.
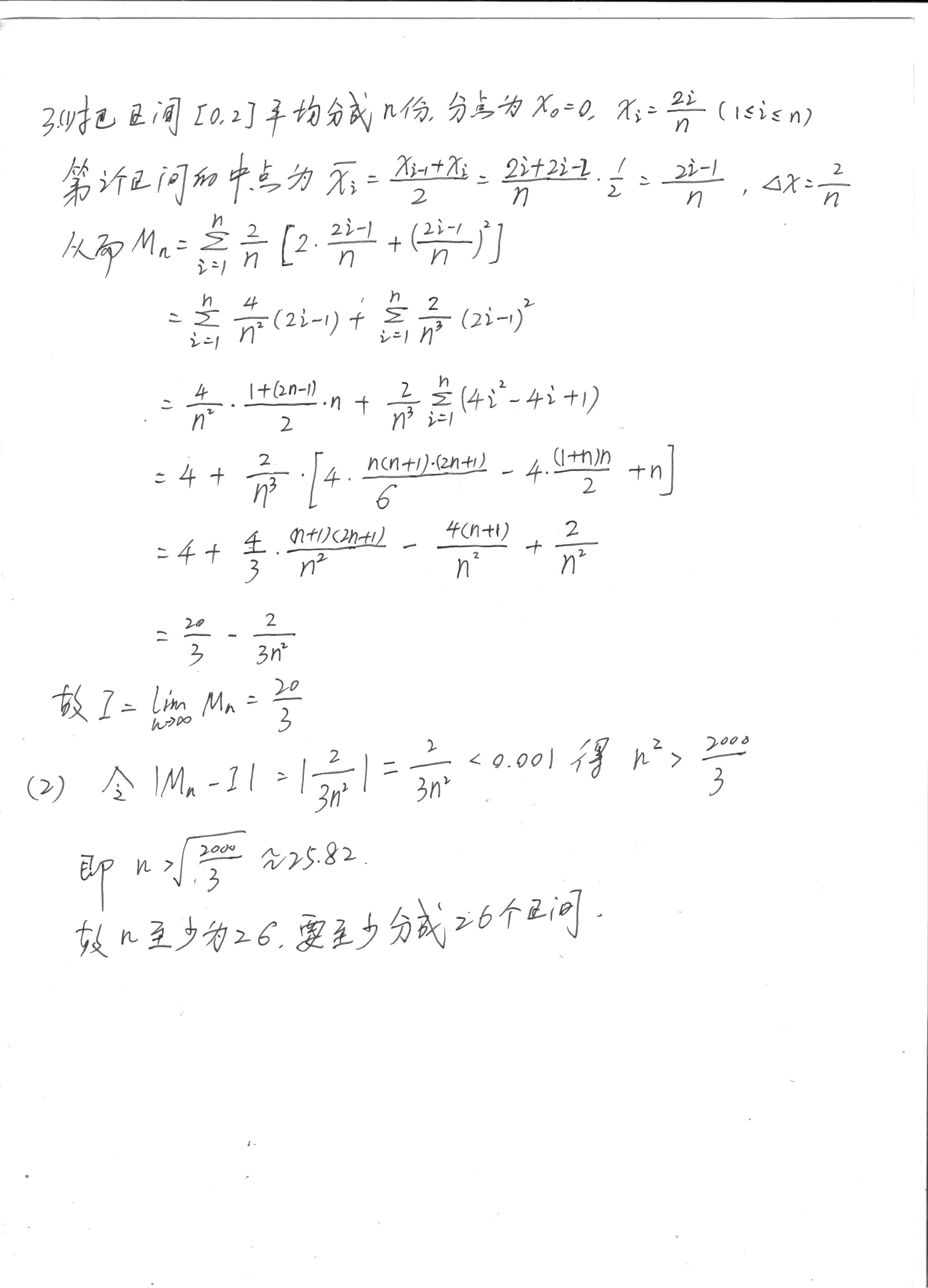
 可以更快获取解答(请注明
可以更快获取解答(请注明