设x→∞lim(x+c/x-c)^x=∫_-∞^cte^2tdt,求c
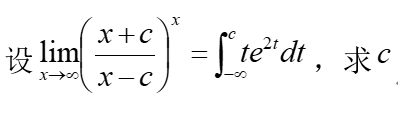
设$\underset{x\to \infty }{\mathop{\lim }}\,{{\left( \frac{x+c}{x-c} \right)}^{x}}=\int_{-\infty }^{c}{t{{e}^{2t}}dt}$,求 $c$
$\lim _{x \rightarrow \infty}\left(\frac{x+c}{x-c}\right)^x=\lim _{x \rightarrow \infty}\left(1+\frac{2 c}{x-c}\right)^{\frac{x-c}{2 c} \cdot \frac{2 c x}{x-c}}=e^{2 c}$
$又 \int_{-\infty}^c t e^{2 t} d t=\frac{1}{2} \int_{-\infty}^c t d e^{2 t}=\left.\frac{1}{2} t e^{2 t}\right|_{-\infty} ^c-\frac{1}{2} \int_{-\infty}^c e^{2 t} d t=\frac{1}{2} c e^{2 c}-\left.\frac{1}{4} e^{2 t}\right|_{-\infty} ^c=\left(\frac{1}{2} c-\frac{1}{4}\right) e^{2 c}$
由 $e^{2 c}=\left(\frac{1}{2} c-\frac{1}{4}\right) e^{2 c}$ 得 $c=\frac{5}{2}$.
添加微信 可以更快获取解答(请注明有偿答疑)
可以更快获取解答(请注明有偿答疑)
最后修改于2024年01月06日
前一篇:判断级数是否收敛?
下一篇:求导公式总结