问题296: Consider A,B∈Rn×n . Suppose that A and B are similar. Show that there is an invertible matrix S such that Null(B)={x∈Rn∣∃y∈ Null(A),x=S−1y}

Question 3. Consider $A, B \in R ^{n \times n}$. Suppose that $A$ and $B$ are similar.
- Show that $A^2$ and $B^2$ are similar.
- Show that, for any integer $n \geq 3, A^n$ and $B^n$ are similar.
- Show that, if $A^2=I$, then $B^2=I$.
- Show that, if $A$ is invertible, then $B$ is invertible and $A^{-1}$ and $B^{-1}$ are similar.
- Show that there is an invertible matrix $S$ such that $\operatorname{Null}(B)=\left\{x \in R ^n \mid \exists y \in\right.$ $\left.\operatorname{Null}(A), x=S^{-1} y\right\}$.
- Show that $n(A)=n(B)$ and $\operatorname{rank}(A)=\operatorname{rank}(B)$.
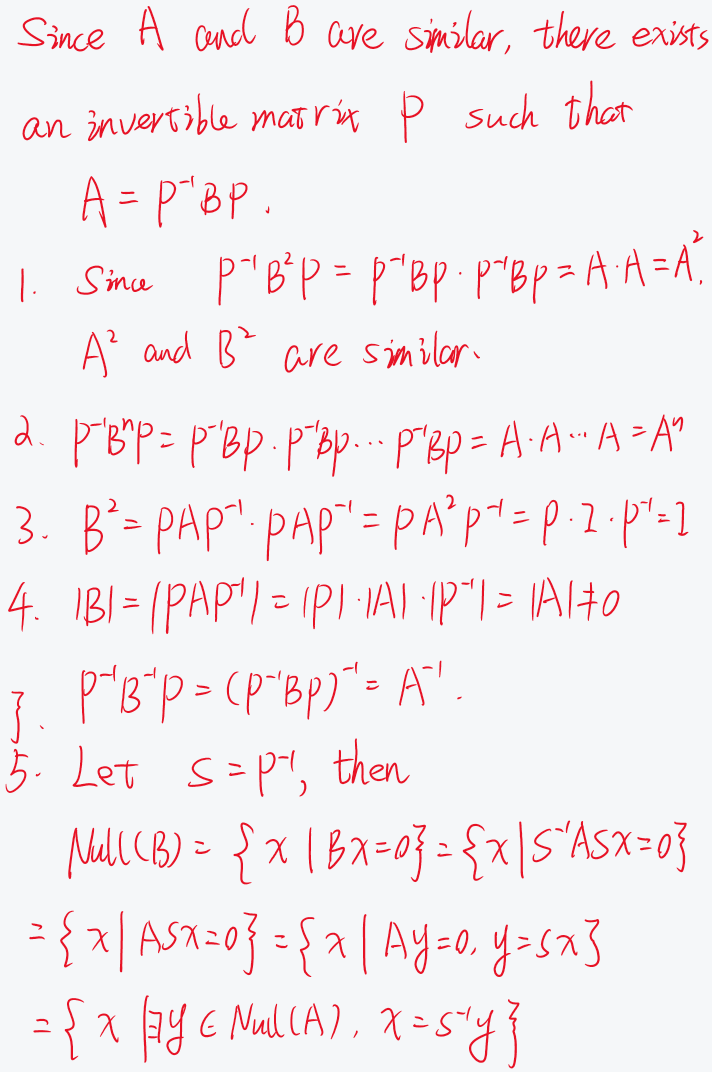

 可以更快获取解答
可以更快获取解答