问题294: Assume everything converges. (i) (2 pts) For n∈N , show that if f(x)=f(1/x) ,
Assume everything converges.
(i) (2 pts) For $n \in N$, show that if $f(x)=f(1 / x)$,
$$ \int_0^{\infty} \frac{f(x)}{1+x^n} \frac{ d x}{x}=\frac{1}{2} \int_0^{\infty} f(x) \frac{ d x}{x} $$
(ii) (2 pts) For $n \in N$, evaluate
$$ \int_0^{\infty} \frac{ d x}{\left(1+x^n\right)\left(1+x^2\right)} $$

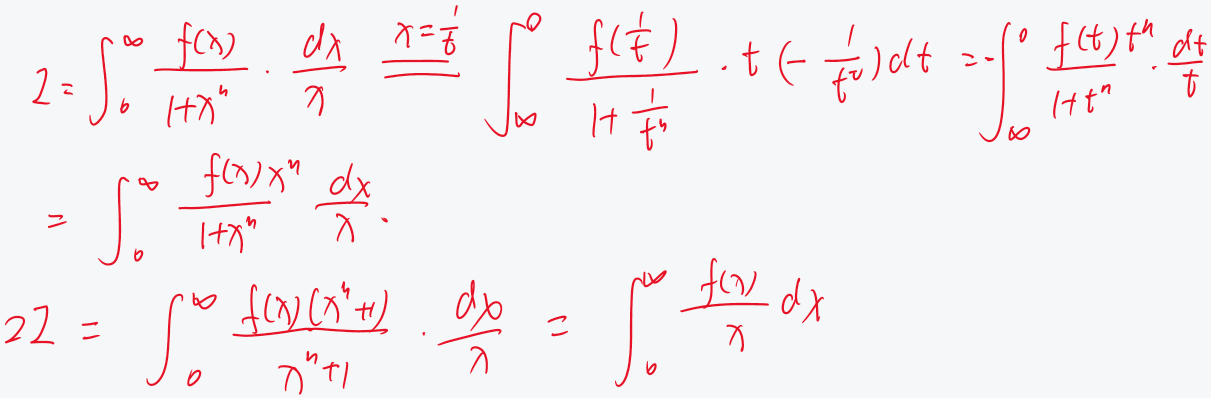
 可以更快获取解答
可以更快获取解答