问题286: 求将 y=x3 和 y=4x2 围成的区域绕 y=−1 直线旋转得到的立体体积:
- 求将 $y=x^3$ 和 $y=4 x^2$ 围成的区域绕 $y=-1$ 直线旋转得到的立体体积:
(a) 使用 $x$ 作为积分变量。
(b) 使用y作为积分变量。 - 设favg[a，b] 表示 $f$ 在区间 [a, b] 上的平均值。如果 $a<c<b$, 那么
问题
解答
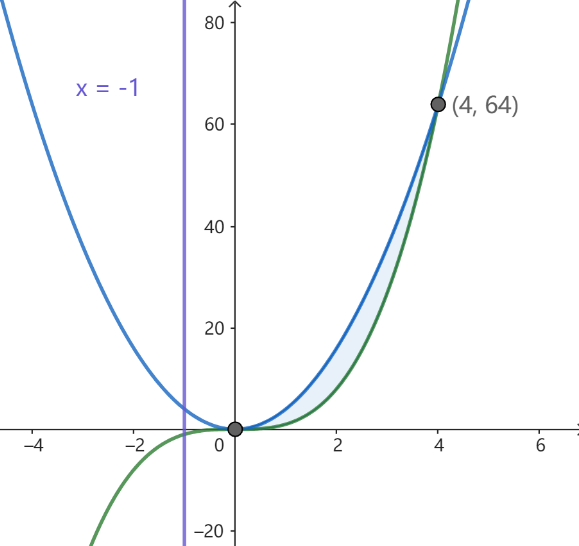
a) $V=\int_0^4\left(4 x^2-x^3\right) \cdot 2 \pi(x+1) d x=\frac{2176}{15} \pi$
b) $V=\int_0^{64} \pi(\sqrt[3]{y}+1)^2-\pi\left(\frac{\sqrt{y}}{2}+1\right)^2 d y=\frac{2176}{15} \pi$
添加微信
可以更快获取解答（请注明有偿答疑）
最后修改于7月3日
提交新的问题
前一篇：问题285: 皇仁酒樓今年春季出售一批野生忘不了魚。因忘不了是從朋友手上活得的關係,而淨料率 85 %。
下一篇：问题287: 请将1/2x+3/4y−1=5/6x+2/3y−1/3变形为y=〇〇。