问题284: 证明行列式=x^n+a1x^n−1+⋯+an−1x+an .

证明 $\left|\begin{array}{cccccc}x & -1 & 0 & \cdots & 0 & 0 \\ 0 & x & -1 & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & \cdots & x & -1 \\ a_n & a_{n-1} & a_{n-2} & \cdots & a_2 & x+a_1\end{array}\right|=x^n+a_1 x^{n-1}+\cdots+a_{n-1} x+a_n$.
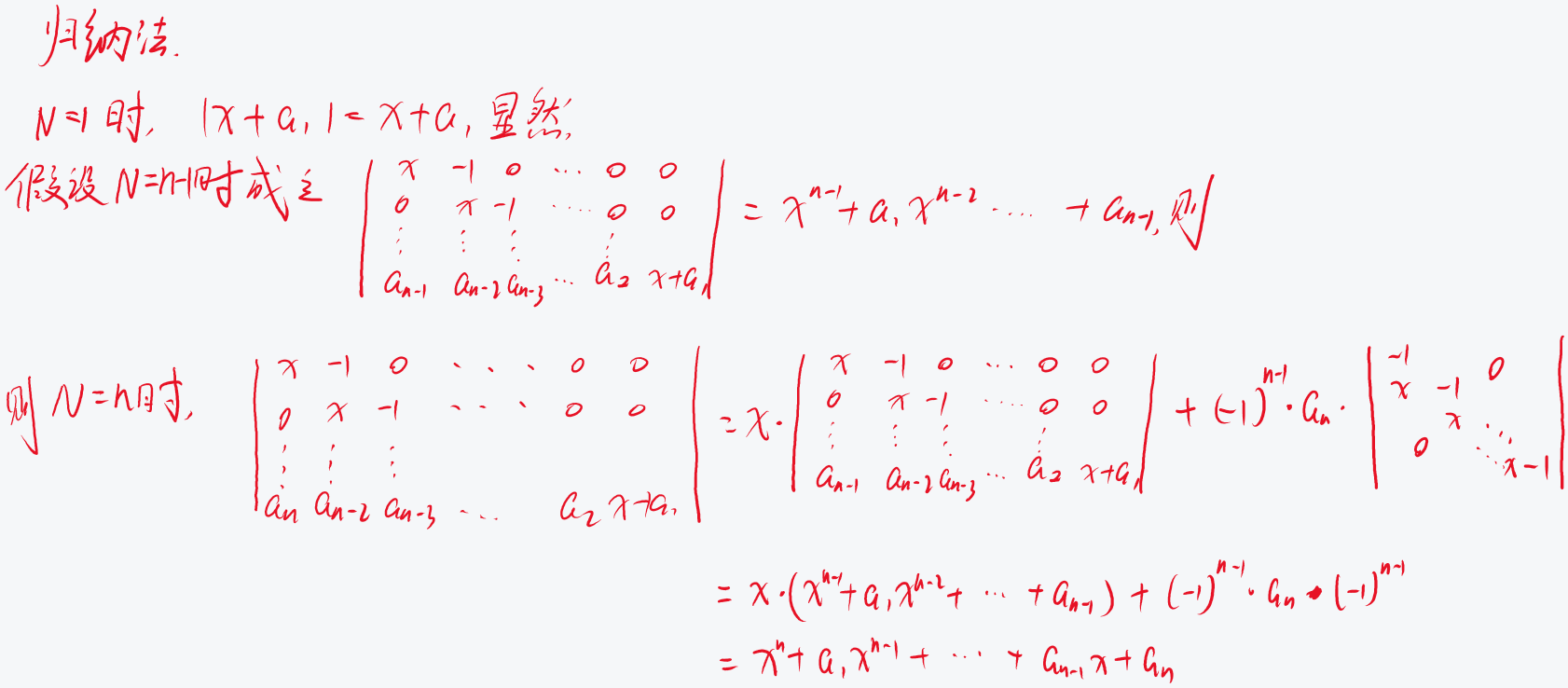
 可以更快获取解答
可以更快获取解答