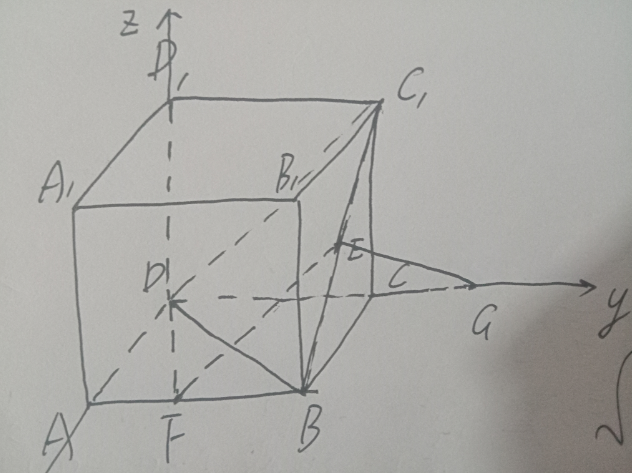
问题232: 如图，在正方体 ABCD−A1B1C1D1 中, E,F 分别为 BC1,AB 的中点, G在DC的延长线
如图，在正方体 ABCD−A1B1C1D1 中, E,F 分别为 BC1,AB的中点, G在DC的延长线
上, 且 CG=12CD.
(1) 证明: EG⊥ 平面 BC1D.
(2)求平面 BC1D 与平面 DEF 的夹角的余弦值.
问题
解答
添加微信
可以更快获取解答（请注明有偿答疑）
最后修改于2024年03月27日
提交新的问题
前一篇：问题230: 比如 一公斤矿石里有百分之65%是铁矿石的情
下一篇：问题233: 已知等轴双曲线 C:x^2/a^2−y^2/b^2=1(a>0,b>0) 的焦距 2√6 .