计算I=∫arccote e^x/e^x d x
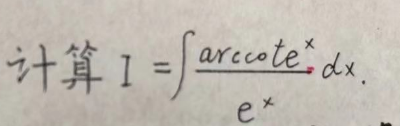
计算$ I=\int \frac{\operatorname{arccote} e^x}{e^x} d x$
$$ \begin{aligned} I & =-\int \arctan e^{-x} d e^{-x} \\ & =-e^{-x} \arctan e^{-x}-\int \frac{e^{-x}}{1+e^{-2 x}} d x \\ & =-e^{-x} \arctan e^{-x}+\frac{1}{2} \int \frac{d e^{-2 x}}{1+e^{-2 x}} \\ & =-e^{-x} \arctan e^{-x}+\frac{1}{2} \ln \left(1+e^{-2 x}\right)+c \end{aligned} $$
添加微信 可以更快获取解答
可以更快获取解答
最后修改于2023年05月20日
下一篇:mathematica基本操作