求积分∫1/(1+e^x)^2 d x
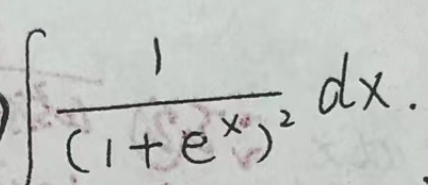
$\int \frac{1}{\left(1+e^x\right)^2} d x$
$\begin{aligned} 原式 & =\int \frac{1+e^x-e^x}{\left(1+e^x\right)^2} d x \\ & =\int \frac{1}{1+e^x}-\frac{e^x}{\left(1+e^x\right)^2} d x \\ & =\int \frac{1}{1+e^x} d x-\int \frac{d\left(e^x+1\right)}{\left(1+e^x\right)^2} \\ & =\int \frac{d e^x}{e^x+\left(e^x\right)^2}+\frac{1}{1+e^x} \\ & =\int\left(\frac{1}{e^x}-\frac{1}{e^x+1}\right) d e^x+\frac{1}{1+e^x} \\ & =\ln e^x-\ln\left(e^x+1\right)+\frac{1}{1+e^x}+C \\ & =x-\ln \left(e^x+1\right)+\frac{1}{1+e^x}+C\end{aligned}$
添加微信 可以更快获取解答(请注明有偿答疑)
可以更快获取解答(请注明有偿答疑)
最后修改于2023年05月20日