问题176: 求过 B(−2.3) 且与圆 x^2+y^2−5x+4y−35=0 相切的直线方程式 9x−10y+48=0

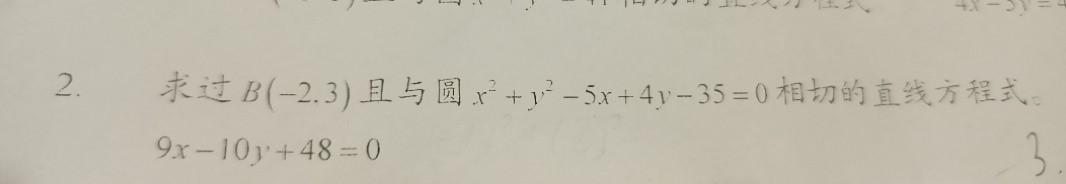
圆方程可化为 $\left(x-\frac{5}{2}\right)^2+(y+2)^2=\frac{181}{4}$ ，圆心O ( $\left.\frac{5}{2},-2\right)$.

B点坐标代入圆方程， $(-2)^2+3^2+5\cdot 2+4 \cdot 3-35=0$, 从而B在圆上，故B是切点, 从而切线与OB重直。

OB斜率为 $\frac{3+2}{-2-\frac{5}{2}}=-\frac{10}{9}$.

切线斜率为 $-\frac{1}{-\frac{10}{9}}=\frac{9}{10}$

切线方程为 $\frac{y-3}{x+2}=\frac{9}{10}$.

即 $9 x-10 y+48=0$ 。

添加微信可以更快获取解答（请注明有偿答疑）