由曲线y=x^2( x ≥ 0 )以及曲线在x=a( a > 0 )处的切线和x轴围成的区域记为D. 若D分别绕x轴和 y 轴旋转一周所得的两个立体体积相同, 则a=( )

分析

本问题考察旋转体体积计算。

先求出切线方程，得到切线与$x$轴的交点坐标，然后分别计算旋转体体积，令它们相等，即可求出$a$的值。

其中，旋转体体积计算公式为：

$y=f(x)$绕$x$轴旋转：$V_x=\int_a^b\pi f(x)^2 \mathrm{d}x$

$y=f(x)$绕$y$轴旋转：$V_y=\int_a^b 2 \pi x f(x) \mathrm{d}x$

$x=f(y)$绕$x$轴旋转：$V_x=\int_a^b 2 \pi y f(y) \mathrm{d}y$

$x=f(y)$绕$y$轴旋转：$V_y=\int_a^b\pi f(y)^2 \mathrm{d}y$

解答

根据题意绘图如下：

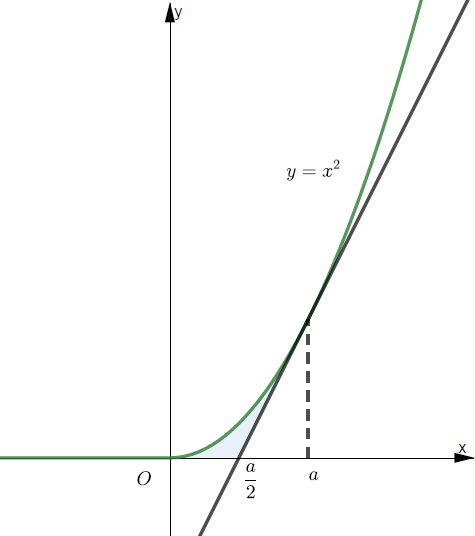
由$y=x^2$得$y^{\prime}=2 x$，从而曲线在$x=a$处切线方程为$y=2 a(x-a)+a^2$，即$y=2 a x-a^2$。切线与$x$轴交点为$\left(\frac{a}{2}, 0\right)$,
从而区域$D$绕$x$轴旋转体积为
$\begin{aligned} V_x & =\pi \int_0^a x^4 d x-\pi \int_{\frac{a}{2}}^a\left(2 a x-a^2\right)^2 d x \\ & =\frac{\pi}{5} a^5-\pi a^2 \int_{\frac{a}{2}}^a\left(4 x^2+a^2-4 a x\right) d x \\ & =\frac{\pi}{5} a^5-\left.\pi a^2\left(\frac{4 x^3}{3}+a^2 x-2 a x^2\right)\right|_{\frac{a}{2}} ^a \\ & =\frac{\pi a^5}{30}\end{aligned}$

区域$D$绕$y$轴旋转体积为
$\begin{aligned} V_y & =2 \pi \int_0^a x \cdot x^2 d x-2\pi \int_{\frac{a}{2}}^a x \cdot\left(2 a x-a^2\right) d x \\ & =2 \pi \cdot\left(\frac{a^4}{4}-\frac{5}{24} a^4\right) \\ & =\frac{\pi a^4}{12}\end{aligned}$

由$\frac{\pi}{30} a^5=\frac{\pi}{12} a^4$，
得$a=\frac{5}{2}$。

添加微信可以直接提问（请注明数学答疑）

最后修改于2023年05月20日