问题120: 什么是四分位数? 如何计算四分位数?

四分位数的定义

四分位数是把所有数据排序后分成四等份, 处于分割点的数就是四分位数.

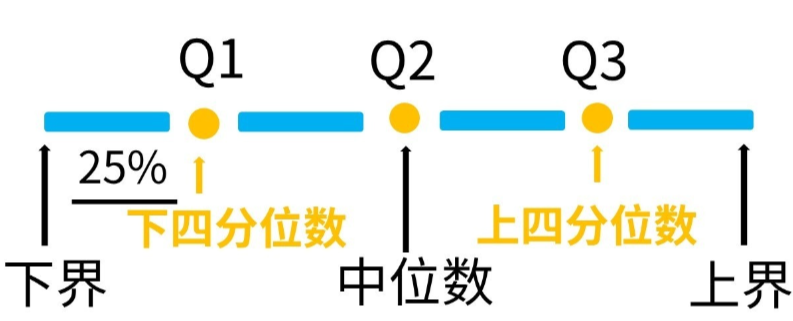
• 第一四分位数, 也叫下四分位数, 或者25%分位数, 是所有数据排序后, 位于25%位置的数
• 第二四分位数, 就是通常所说的中位数, 是所有数据排序后, 位于50%位置的数
• 第三四分位数, 也叫上四分位数, 或者75%分位数, 是所有数据排序后, 位于75%位置的数

第三个四分位数与第一个四分位数的差叫四分位距

计算中位数

• 如果一组数据的个数$n$是奇数, 那么中位数就是正中间那个数, 也就是第$\frac{n+1}{2}$个数
• 如果一组数据的个数$n$是偶数, 那么中位数就是正中间两个数的平均值, 也就是第$\frac{n}{2}$个数和第$\frac{n+2}{2}$个数的平均值

计算上四分位数和下四分位数

对于离散数据而言, 计算上四分位数和下四分位数并没有统一的方法, 常用方法如下

方法一

• 要计算下四分位, 先计算$\frac{n}{4}$, 如果$\frac{n}{4}$是整数, 则下四分位数是第$\frac{n}{4}$和第$\frac{n}{4}+1$个数的平均值; 如果$\frac{n}{4}$不是整数, 那么下四分位数就是第$[\frac{n}{4}+1]$个数
• 要计算上四分位, 先计算$\frac{3n}{4}$, 如果$\frac{3n}{4}$是整数, 则上四分位数是第$\frac{3n}{4}$和第$\frac{3n}{4}+1$个数的平均值; 如果$\frac{3n}{4}$不是整数, 那么上四分位数就是第$[\frac{3n}{4}+1]$个数

注: 浙大版概率统计和北师版高中数学用方法一计算四分位数

方法二

• 如果数据总数是偶数, 那么中位数把把数据分成了两部分, 下四分位数就是第一部分的中位数, 上四分位数就是第二部分的中位数
• 如果数据总数是$n=4k+1$, 则下四分位数就是第$k$个数值的25%加第$k+1$个数值的75%, 上四分位数就是第$3k+1$个数值的75%加第$3k+2$个数值的25%
• 如果数据总数是$n=4k+3$, 则下四分位数是第$k+1$个数值的75%加第$k+2$个数值的25%, 上四分位数就是第$3k+2$个数值的25%加第$3k+3$个数值的75%

方法三

• 如果数据总数是奇数, 那么中位数把数据分成两部分, 分别计算两部分数据(不含中位数)的中位数就是下四分位数和上四分位数
• 如果数据总数是奇数, 那么中位数把数据分成两部分, 分别计算两部分数据的中位数就是下四分位数和上四分位数

方法四

与方法三类似, 只是在总数是奇数的情形, 包含总体的中位数再计算两部分的中位数

• 如果数据总数是奇数, 那么中位数把数据分成两部分, 分别计算两部分数据(含中位数)的中位数就是下四分位数和上四分位数
• 如果数据总数是奇数, 那么中位数把数据分成两部分, 分别计算两部分数据的中位数就是下四分位数和上四分位数

添加微信可以更快获取解答（请注明有偿答疑）