问题117: 解方程{2/(x+1)+3/(y+1)=1;4/(x−1)−1/(y−3)=1

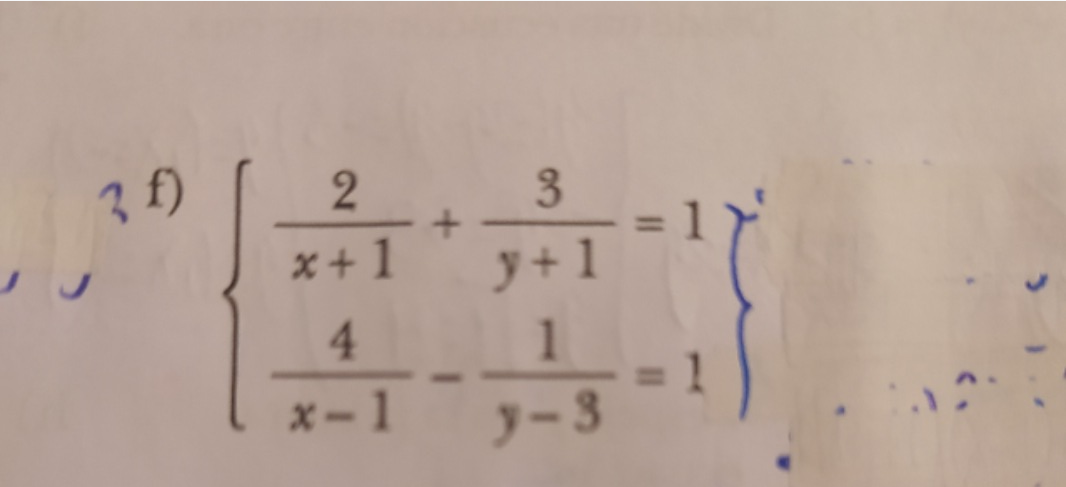
$$ \left\{\begin{array}{l} \frac{2}{x+1}+\frac{3}{y+1}=1 (1)\\ \frac{4}{x-1}-\frac{1}{y-3}=1 (2) \end{array}\right. $$

由(1)得$2(y+1)+3(x+1)=(x+1)(y+1)$,
即 $2 x+ y-x y=-4$ (3)
由(2)得 $\quad 4(y-3)-(x-1)=(x-1)(y-3)$,
即 $2 x+5 y-x y=14$ (4)
(4) -(3) 得 $\quad 4 y=18$
即 $\quad y=\frac{9}{2}$
代入(3)式， $2 x+\frac{27}{2}-\frac{9 x}{2}=-4$
从而 $x=7$
故 $\left\{\begin{array}{l}x=7 \\ y=\frac{9}{2}\end{array}\right.$

添加微信可以更快获取解答（请注明有偿答疑）