反双曲函数及其性质

反双曲函数

$$ \begin{aligned} & \operatorname{arsinh}(x)=\ln \left(x+\sqrt{x^2+1}\right) \\ & \operatorname{arcosh}(x)=\ln \left(x+\sqrt{x^2-1}\right) ; x \geq 1 \\ & \operatorname{artanh}(x)=\frac{1}{2} \ln \left(\frac{1+x}{1-x}\right) ;|x|<1 \end{aligned} $$

反双曲函数图像

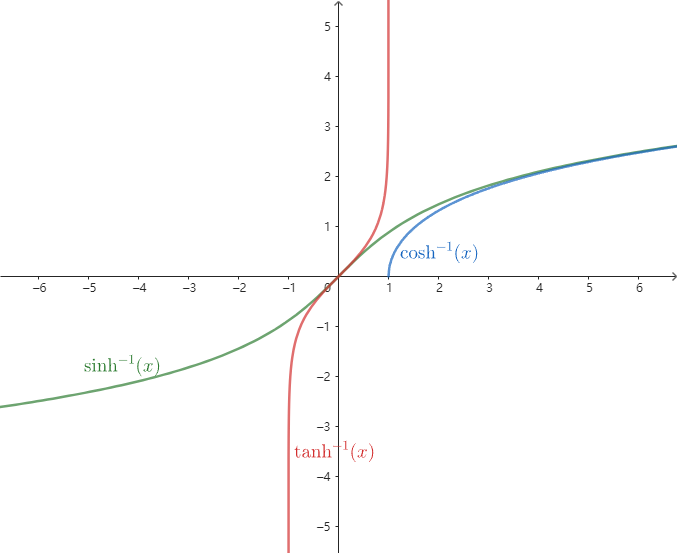
从图像可以看出, 反双曲正弦和反双曲正切都是奇函数, 且都是单调递增的函数.

反双曲函数的导数

$$ \begin{aligned} & (\operatorname{arsinh} x)^{\prime}=\frac{1}{\sqrt{1+x^2}} \\ & (\operatorname{arcosh} x)^{\prime}=\frac{1}{\sqrt{x^2-1}} \\ & (\operatorname{artanh} x)^{\prime}=\frac{1}{1-x^2} \end{aligned} $$